- Szerző admin [email protected].
- Public 2023-12-16 19:22.
- Utoljára módosítva 2025-06-01 06:12.

Az aranymetszés példái mindenhol megtalálhatók a klasszikus építészetben, a műalkotásokban, a természetben és még a zenében is. Az arányoknak ez a kifejezése, más néven isteni arány, harmonikus kompozíciót kínál egy irracionális szám (1,618) alkalmazásával a tervezésben, mind a természetes, mind az ember által alkotott formában. Valószínűleg nincs tisztában az aranymetszés szépsége mögött meghúzódó matematikával, mert olyan tárgyakat és zenét hoz létre, amelyeket természetesen tetszetősnek találsz, minden magyarázat nélkül.
Arany arány az építészetben
Az aranymetszés csaknem tökéletes szépséget teremt a természetben és a művészetben. Amikor elkezdi keresni az Arany arány példáit a mindennapi életben, meglepődhet azon, hogy számos monumentális épület és építmény létrehozására használták fel. Amikor az Arany Arányt használják az építészetben, az épületről azt mondják, hogy a "szakrális építészet" felhasználásával hozták létre. Az Arany arány számításának egy négyzetre történő alkalmazásával az építészek és a tervezők létrehozhatják az Arany Téglalapot, amelyről úgy tartják, hogy az emberi szem számára a legesztétikusabb arányokkal rendelkezik.
Arany téglalap Példa: A Parthenon

Phidias, a görög szobrász az Aranymetszetet használta munkáiban, különösen akkor, amikor a Parthenon-oszlopok fölött faragott szalagokkal kezdett dolgozni. Azt is fontos megjegyezni, hogy az aranyarányhoz rendelt számértéket, a Phi-t az ő tiszteletére nevezték el.
Ha megméred a Parthenon külső méreteit, rájössz, hogy nem csak egy arany téglalapot alkot, hanem az oszlopok között sok arany téglalap is található. Ez a szakrális építmény az építészet aranyarányának gyönyörű példája.
Arany háromszög Példa: Gízai nagy piramis
Az aranyarány, az arany téglalap és az arany háromszög mind megtalálható a világ hét csodájának egyikében, a gízai nagy piramisban. Az aranyarány meghatározásához fel kell vágnia a piramis négyzetes alapját, és függőleges vonalat kell húznia a piramis közepére. Ha ez a piramis szögletes oldalához kapcsolódik, akkor könnyen láthatja, hogyan alkotja meg az 1,618-as arányú Arany Háromszöget, az Aranyarányt.
Egyéb építészeti példák
Sok példát találhat az ősi és a modern szakrális építészetre és az Arany arányú épületekre.
- Chartres-i katedrális - központ, Franciaország
- Notre Dame - Párizs, Franciaország
- Porch of Maidens - Akropolisz, Athén
- Taj Mahal - Agra, India
- United Nations Building - New York City, New York
Arany arány a művészeti példákban
Sok példát találhat olyan festőmesterektől, akik az Aranymetszetet használták. Ezek a tökéletes alkotások az arany téglalapok és az arany háromszögek arányának felhasználásával készültek. Az Arany Téglalap alapján létrehozott művészet kellemesebbnek bizonyul az emberi szem számára. Ez az egyik rejtély, amely körülveszi ezt a tökéletes téglalapot és az aranyarányt.
Arany arány a művészetben

Aranymetszés művészeti példák:
- Leonardo Di Vinci - Mona Lisa, Vitruvius Man
- Botticelli - Vénusz születése
- Michelangelo - Szent Család, 'Dávid'
- Raphael - Keresztrefeszítés
- Rembrandt - Önarckép
- Salvador Dali - Az utolsó vacsora szentsége, Az emlékezet megmaradása
Arany arány használata a műalkotásban
Az arany téglalapon belül vannak bizonyos területek, amelyek vizuálisan vonzóbbak, mint más területek. Ezeket a pontokat úgy fedezhetjük fel, hogy a téglalap alsó sarkából vonalat húzunk a másik sarokba, és megismételjük a másik alsó sarokkal. Ezek a vonalak az arany téglalap pontos középpontjában metszik egymást. Ezután mérje meg a középső ponttól kezdve minden vonal mentén a felezőt. Ezt a négy pontot nevezzük a téglalap szemének (arany arány). A festmény fő fókuszpontja ezután ezeken az érdeklődési pontokon (arányokon) belül kerül megrajzolásra vagy festésre.
Arany arány a zenében

A zene számértékekből áll, és ha az aranymetszetet felhasználják egy zenemű létrehozásához, az a matematika élő példája lesz. A Fibonacci-szekvencia a zenében is elterjedt:
- Egy skálán nyolc hang található.
- A harmadik és kvint hang az akkordok alapja.
- Bármely hang hossza vagy oktávja 13 hang.
A szekvenálás az egész zeneműben folytatódik, és egyre összetettebbé válik, ahogy eléri az aranyarányt.
Az aranymetszetet használó zeneszerzők
Néhány legismertebb klasszikus zeneszerző az Aranymetszetet és a Fibonacci-sorrendet használta zenei darabjaiban, köztük Bach, Beethoven, Chopin és Mozart. Néhány modern zeneszerző, mint például Casey Mongoven, feltárta zenéjében az Arany arányt.
Aranyarány-példák a természetben

Hol található a természetben az aranymetszés? Az Arany- vagy Fibonacci-spirálban van, amely az Aranyarány használatával hozható létre. Ez egy olyan jelenség, amely széles körben megtalálható a természeti világban. A növény levelei úgy nőnek, hogy a lehető legtöbben felfelé ívelhessenek a száron. Új levél csak azután alakul ki, amelyik továbbhaladt.
- Spirális kaktuszok
- Spirálgalaxisok
- Napraforgók
Virágok Fibonacci-szekvenciával
Egyes virágok virágszirmai a Fibonacci-szekvenciát követik:
- Három szirom:Íris, liliom, orchidea, trillium
- Öt szirom: Boglárka, muskátli, hibiszkusz, hajnalka, nasturtium
- Nyolc szirom: Delphiniumok
- 13 szirom: Egyes százszorszépfajták, parlagfű, körömvirág
Fibonacci spirál fenyőtobozban

Fafajtától függően a Fibonacci-számsorozaton belül a fenyőtobozokban is látható az aranyarány. A fenyőtoboz egyik oldalán nyolc spirálból álló sorozat található, a másik oldalon 13 spirál. Egy másik fenyőtoboz minta egyik oldalán öt spirál, a másikon nyolc spirál található.
Arany arány az emberekben
Ez az arány nemcsak abból a szempontból fontos, hogy az emberek hogyan tekintenek egymásra, hanem a testük működésére és a DNS-ükre is.
DNS felfedi az aranyarányt
Az aranyarány egyik legcsodálatosabb példája az emberi DNS szerkezetében található. Ez egyetlen DNS-keresztmetszeten látható, amely felfedi, hogy a DNS kettős hélix tízszög alakú. Ez két, egymástól 36 fokkal elforgatott ötszög kombinációja alkotja a DNS kettős hélixet. Maga a kettős hélix spirál ötszöget alkot. Még egyetlen DNS-molekula is felfedi az aranymetszet vagy az isteni arány alapját.
Matek az aranyarány mögött
Az aranymetszet megtalálása a való életben egyszerű, hiszen az mindenhol megjelenik körülötted. Ez egy matematikai közhely, amelyet az emberek által évszázadok óta lemásolt és utánzott természetben található tökéletes szám meghatározására használnak. Ennek a számnak a leegyszerűsített szépsége álcázza a végrehajtás bonyolultságát. Ahhoz, hogy megértsük az aranymetszés mögötti elméletet, először fel kell fedeznünk az arány Fibonacci-sorrendjét.
Fibonacci-szekvencia és az aranyarány
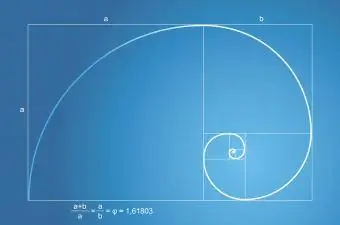
A Fibonacci-sorozatnak vagy sorozatnak van kapcsolata az aranyaránnyal. A Fibonacci-sorozat a növény leveleinek és a virág szirmainak számában jelenik meg. A természetben található Fibonacci spirál mindig egy aranyarányú arany téglalap része.
A Fibonacci-sorozat matematikája egyszerű:
- A sorozat 0-val és 1-gyel kezdődik.
- Csak add össze az utolsó két számot, hogy megkapd a sorozat következő számát.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 és így tovább.
- A Fibonacci sorozat példája a következő lesz: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 és így tovább.
A Fibonacci és az Aranymetsző kapcsolata akkor valósul meg, ha előre, tovább és tovább adják. Minél több sorozatot ad hozzá, annál közelebb kerül az aranyarányhoz.
Arany téglalap és háromszög létrehozása
Arany téglalap létrehozásához a Fibonacci-szekvenciával kezdje egy négyzettel. Elkezd egy téglalapot építeni úgy, hogy hozzáad egy másik négyzetet az eredeti négyzethez. Ne felejtse el használni a következő képletet: 0+1=1 az első négyzet, 1+1=2 - újabb négyzetet ad hozzá.1+2=3 három négyzetet ad hozzá, majd 2+3=5, öt négyzetet. Továbbra is hozzáadhat négyzeteket, és végül egy arany téglalapot hoz létre.
Arany háromszög hozható létre úgy, hogy egy Arany Téglalapot kettévág az egyik sarkából a másik sarokba. Ez egy olyan háromszöget hoz létre, amelynek három oldala vagy szögei 2:2:1 arányúak, ami azt jelenti, hogy a két hosszú oldal egyenlő hosszú, a rövid szög pedig pontosan fele a két hosszabb oldal hosszának.
Arany arány a Való Világban
Az aranyarányt gyakran isteni aránynak nevezik, mert kiemelkedő a természetben és az emberi testben. Az a felfedezés, hogy az aranymetszés oly sok élőlényben jelen van, elősegítette ennek a varázslatos aránynak a tiszteletét, és ma is ihletet ad a művészeknek és alkotóknak.






